 |
Mathematics 308 Project: |
 |
 |
Mathematics 308 Project: |
 |
According to David Eppstein, a tiling is "a partition of an infinite space (usually Euclidean) into pieces having a finite number of distinct shapes" (Eppstein, The Geometry Junkyard: Tiling). Basically, a tiling of the plane involves fitting two-dimensional shapes (from a finite set of distinct shapes) onto the plane such that the shapes don't overlap and there are no holes.
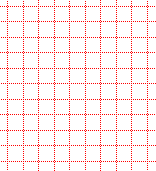
A periodic tiling is one in which the tiles form a pattern which repeat themselves periodically. By contrast, an aperiodic tiling is one in which the tiles don't quite form a repeating pattern.
 |
 |
A periodic tiling (left) and an aperiodic Penrose Tiling (right).
Roger Penrose found that given two tiles, a kite and a dart, and a set of matching rules for them, these two tiles could only tile the plane aperiodically. A tiling made of these two tiles (including their matching rules) and other variants, of which the most famous are the set of two "Penrose" rhombuses, is called a Penrose Tiling.

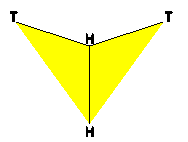
A kite (left) and a dart (right), made from parts of "Penrose" rhombuses. The matching rules are represented by H and T labels, where corners that meet must have the same letter (for more details, see Gardner, Penrose Tiles to Trapdoor Ciphers, p.6-7).
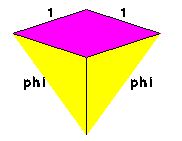
A thin rhombus (left) and a fat rhombus (right). The interior angles are labelled (in degrees). The matching rules are represented by the arrows. Edges that meet must have the same number of arrows and these arrows must point in the same direction (these matching rules are shown Fig. 6.5 of Senechal, Quasicrystals and Geometry, p.175).
The golden ratio is:
The kites and darts of the original Penrose Tiling both have two long edges and two short edges each. In fact, in "unit" kites and darts, a short edge has a length of 1 unit, while a long edge has a length of "golden ratio" units (about 1.618). Martin Gardner also noticed that the ratio of kites to darts in a Penrose Tiling is the golden ratio (see Gardner, Penrose Tiles to Trapdoor Ciphers).
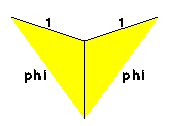
A kite (left) and a dart (right), made from parts of "Penrose" rhombuses. The edge lengths are labelled ("phi" represents the golden ratio).
The fat and thin "Penrose" rhombuses are also closely related to the golden ratio. All of the interior angles the rhombuses are multiples of 36 degrees, whose cosine is half of the golden ratio (as shown in the formula above). (These interior angles are 36 and 144 degrees for the thin rhombus, and 72 and 108 degrees for the fat rhombus, as shown in the picture in the previous section.) A second interesting fact is that the ratio of the fat rhombus' long diagonal to its short diagonal is the golden ratio.
In fact the deflation algorithm for tiling a "Penrose"
rhombus, as shown in the next section, recursively tiles over the "current"
tiles with new smaller tiles whose sizes are
In fact, Martin Gardner says that the irrationality of the golden ratio underlies Penrose's proof that a Penrose tiling is always nonperiodic (Gardner, Penrose Tiles to Trapdoor Ciphers, p.7).
Because there is no strict pattern in a Penrose Tiling (even though there may be local patterns), it is hard to do a correct Penrose Tiling by simply placing a "Penrose" rhombus in the center and trying to tile around it.
On the other hand, a "Penrose" rhombus can be deflated by recursively cutting it up into smaller penrose rhombuses (along with some half-rhombuses along the edge of the original rhombus).
Tilings of a thin rhombus (left) and a fat rhombus (right) by thin and fat rhombuses (with some half rhombuses at edges), with 6 levels of deflation.
This algorithm is based on the one used by Duane Bailey in his Postscript Program to Generate Penrose Tilings.
Instead of using full rhombuses, the deflation algorithm uses half rhombuses. The thin rhombus is cut along its short diagonal and the fat rhombus is cut along its long diagonal.
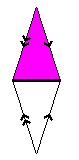
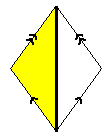
Cutting a thin rhombus (left) and a fat rhombus (right) into half rhombuses (colored parts). Note how each half rhombus (even when enhanced with the matching rule arrows) reflects across the "cut line" to produce the other half of the rhombus.
These half rhombuses can be fitted with Robinson tiles. The four Robinson tiles are:
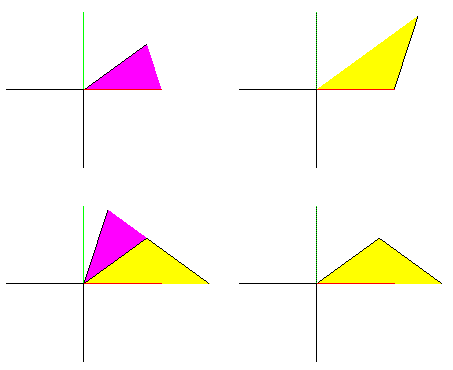
The four Robinson tiles: a half thin (top left), a half fat (top right), a half kite (bottom left), and a half dart (bottom right). These tiles are "unit-sized" and oriented in the "default" manner. The x and y-axes have also been drawn for each figure (positive x-axis in red, positive y-axis in green).

By reflecting the half thin about the y-axis and scaling it by a factor of the golden ratio (and by further translation along the x-axis), we get the half kite. Thus, the half thin and the half kite are congruent.

By rotating the half fat by 144 degrees, we see that the half fat is congruent to the half darts.
The algorithm starts by splitting a rhombus into its two halves (i.e. a thin rhombus is split into two half thins). It then splits each half into a combination of smaller Robinson tiles, which is really a combination of small half fats and small half thins. These small pieces are themselves recursively split into smaller half fats and half thins, and so on, until we decide that we don't want the pieces to get any smaller. As each recursive call returns, these smaller pieces are "glued" back into the larger pieces (or drawn on the screen) and we end up with the two original half rhombuses, which are "glued" together to form the original rhombus.
In fact, it is interesting to note that at each recursive stage, the pieces
are
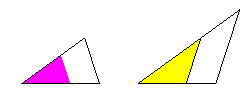
Scaling of a half thin (left) and a half fat (right). The colored part is the scaled tile. The outline is the original tile.
Ignoring reflections, rotations, and translations, we have the following deflation for a half thin:

Deflation of a half thin, by the formula above.
Ignoring reflections, rotations, and translations, we have the following deflation for the half fat:
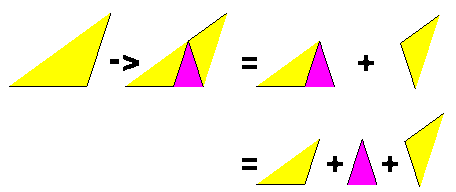
Deflation of a half fat, by the formula above.

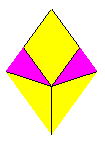
The final results after one level of deflation. (The thin rhombus is on the left and the fat rhombus is on the right.)
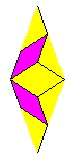
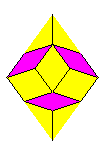
The final results after two levels of deflation. (The thin rhombus is on the left and the fat rhombus is on the right.)
Even though it is hard to see if we only do one level of deflation, a fascinating property of the deflation algorithm is the fact that when the little pieces are "glued" back together to form the bigger pieces (and eventually the original rhombus), they are glued in such a way that all of the half fats and half thins (except some at the edge of the original rhombus) pair up with other half fats and half thins (respectively) to form fat and thin rhombuses.
A second fascinating (but expected) property is that by deflating the rhombuses with this algorithm, the resulting tiling does not have a periodically repeating pattern, no matter how many levels of deflation that you do.
Thus, these two properties show that the algorithm does correctly generate a Penrose Tiling of the plane. This is evident in the tilings of the thin and fat rhombuses at the beginning of this section.
My program that generated the penrose images with the help of the deflation algorithm is penrosedeflate.ps, which is largely based on the Postscript Program to Generate Penrose Tilings, by Duane A. Bailey of Williams College in Williamstown, Massachusetts. The program that generated the periodic grid tiling is periodicgrid.ps.
Java Penrose Tiler, by Geert-Jan van Opdorp. This is an interactive Java applet that lets you try your hand at tiling the plane with kites and darts. There is also an option to view the tiling as rhombuses, but each piece to put on is still a kite or dart.
Clusters and Decagons, by Ivars Peterson. This article in the October 12, 1996 issue of Science News Online examines the relationships between quasicrystals and Penrose Tilings.
The Geometry Junkyard: Penrose Tiles, by David Eppstein. This site has links to other sites that deal with Penrose Tiling.
Duane A. Bailey, A Postscript Program to Generate Penrose Tilings, 1995. Found at http://www.cs.williams.edu/~bailey/color-penrose-program.ps
David Eppstein, The Geometry Junkyard: Penrose Tiles, 1997.
David Eppstein, The Geometry Junkyard: Tiling, 1997.
Martin Gardner, Penrose Tiles to Trapdoor Ciphers, published by
W. H. Freeman and Company, New York, 1989. p.1-28
NOTE: This book is a collection of his "Mathematical Games" columns that
were published in Scientific American. Pages 1 to 18 of the book
(Ch.1) is the column on Penrose Tilings that appeared in the January 1977
edition of the magazine.
Marjorie Senechal, Quasicrystals and Geometry, published by Cambridge University Press, 1995. p.170-206
� 1997. ME. (I'm still not telling you who I am!)